تأمّلی بر سرگذشت اواریست گالوا ، ریاضیدان بدشانس فرانسوی

ریاضیدانان بزرگ معمولاً سرگذشتی غیر داستانی دارند. یا به طور دقیق تر ، داستان زندگی آنها را نوآوری ها و دستاوردهای ریاضیاتیشان تشکیل می دهد که غیر ریاضیدان ها به سختی می توانند آن را درک کنند. بزرگترین استثناء در این قاعده ، اواریست گالوا است. آنچه از زندگی گالوا می دانیم بیشتر شبیه به یک داستان رمانتیک و بلکه تراژدی است. زیرا در تراژدی حتماً نباید قهرمان داستان به طرز فجیعی کشته شود بلکه تراژدی را می توان به عنوان سرکوب نمودن نبوغ یک نابغه و در نظرنگرفتن و توجّه نکردن به او نیز دانست.
اواریست گالوا را حتّی کسانی که دستی بر ریاضیات دارند هم ، نمی شناسند چه رسد به افراد عادّی که بیشتر ریاضیدانان بزرگ و مشهوری چون نیوتن و اویلر و ... ر می شناسند. اواریست گالوا را حتّی دانشجویان ریاضی هم به خوبی نمی شناسند.
در یکی از روزهای سال 1811 میلادی ، در نزدیکی پاریس ، پسری به دنیا آمد که او را "اواریست" نام نهادند. چون والدین پسر ، خود، افرادی تحصیل کرده بودند ، تا سنّ 12 سالگی نزد مادرش به تحصیل و فراگیری علم پرداخت. پس از آن به مدرسه رفت. در دروس عادّی مدرسه دانش آموزی متوسّط بود. امّا هنگامی که کتاب مبانی هندسه اثر «لژاندر» به دستش رسید و آنرا مطالعه کرد به شدّت تحت تأثیر قرار گرفت. می گویند که او این کتاب را مانند یک کتاب داستان عادّی خوانده است و فقط با یک بار مطالعه آن ، بر مطالب کتاب احاطه کامل یافته است. از همین جا بود که با کارهای ریاضیدانان بزرگی چون لاگرانژ و آبل آشنا شد و آنها را مطالعه کرد. هنگامی که 15 ساله شد، خودش به تنهایی یک خواننده حرفه ای آثار ریاضی بود و کشف کردن در دنیای ریاضی را آغاز کرد و به کشفیّات مهمی نیز دست یافت. در آن سنّ و سال کم و بدون بهره بردن از هیچ تحصیلات عالی رسمی ، گالوا قادر بود به کشفیّاتی برسد که او را به شهرتی جاودانه در دنیای ریاضیات برساند. شهرتی که هیچ گاه طعم آنرا در زمان حیاتش نچشید.
"دوپوی" در جمله ای راجع به شرح حال گالوا می گوید:
« کتاب های جبر مقدّماتی هرگز گالوا را قانع نکرد زیرا در آنها جای پایی از مکتشفین نمی یافت. درست از اوّلین سال ریاضی به لاگرانژ روی آورد. »
دست نوشته هایش از نظم و ترتیب خوبی برخوردار نبود و به دلیل ذهن نیرومندی که داشت بیشتر محاسبات ریاضی را به صورت ذهنی انجام می داد و فقط نتایجش را یادداشت می کرد. مقالات و مطالبی که می نوشت مانند اکثر مقالات ریاضیدانان قرن هجدهم ، خلاصه و بی ترتیب بودند. سبک نوشتنی که در ریاضی نویسی امروزی ، کاملاً نامأنوس و نامرسوم است.
مدرسه پلی تکنیک پاریس ، مدرسه ای بود که ریاضیدانان بزرگی در آنجا تربیت شده بودند و دو بار تلاش گالوا برای ورود به این مدرسه، ناکام ماند. گالوا خود به خوبی می دانست که از بسیاری از کسانی که پذیرفته شده بودند ، شایستگی بهتری دارد. امّا او ناامید نشد و خود به مطالعه ریاضی پرداخت. به عقیده بسیاری از ریاضیدانان بزرگ ، پذیرفته نشدن گالوا در مدرسه پلی تکنیک پاریس ، خُسران زیادی برای علم ریاضیات به همراه داشته است.
کشفیّات اساسی او در معادلات چند جمله ای بود که در سال 1829 برای اوّلین بار ، طی مقاله ای ، آنها را به آکادمی علوم پاریس فرستاد. کسی که مقالات ارسالی به آکادمی را از نظر علمی ، قضاوت و داوری می کرد ، "آگوستن لویی کُشی" بود. کُشی ریاضیدان بزرگ و ماهری بود و این توانایی را داشت که بتواند با مطالعه مقاله گالوا ، آنرا بفهمد و به ارزش کشفیّات او پی ببرد. امّا در این بین ، کُشی ، مقاله گالوا را گم کرد و دیگر نتوانست آن را پیدا کند. شاید این گم شدن مقاله را بتوان به حساب بدشانسی خود گالوا گذاشت!!
بعد از این ماجرا ، گالوای شجاع ، کارهایش را در مسابقه سال 1830 جایزه بزرگ آکادمی در ریاضیات شرکت داد. مقاله گالوا بدون شک باید برنده این جایزه می شد. امّا این بار هم بخت با گالوا یار نبود زیرا "فوریه" که منشی آکادمی بود ، مقاله گالوا را با خود به خانه برد و به طور ناگهانی پیش از خواندن آن فوت کرد و مقاله گالوا دوباره گم شد!!
گالوا نسخه دوّم مقاله اش را به آکادمی فرستاد. این بار قضاوت درباره مقاله ، بر عهده "پواسون" بود. هنگامی که پواسون مقاله گالوا را مطالعه کرد ، در حاشیه یکی از برهان های گالوا ، یادداشتی به این مضمون نوشت:
« برهان این هم ناکافی است امّا بنابر بخش 100 از مقاله آقای لاگرانژ ، برلین ، 1771 ، درست است. »
چه اتّفاقی افتاده بود ؟ مگر می شود برهان یک قضیه ، ناکافی امّا درست باشد ؟
گالوا در یادداشتی دست نویس به پواسون پاسخ داد : « اثبات خواهد شد. »
شاید منظور گالوا ، چیزی شبیه به "آن بماند تا ببینیم" بوده است. با این حال منظور گالوا این بوده است که " لطفاً به بررسی بقیه قسمت های مقاله بپردازید تا من برهان را در آینده کامل کنم. "
امّا پواسون در گزارش خود به آکادمی از مقاله گالوا به عنوان یک کلّیت یاد کرده و می نویسد:
« ما تمام کوشش خود را برای درک برهان آقای گالوا به کار بردیم ، امّا استدلال های ایشان به اندازه کافی روشن نیست و به اندازه کافی پرورانده نشده اند تا م بتوانیم درباره درستی آنها قضاوت کنیم ... »
پواسون امیدوار بود که گالوا به اصلاح و توسعه کار عرضه شده خویش بپردازد تا بتواند برهان کاملتری را به آکادمی ارائه دهد. امّا گالوا می دانست که برهانهایش درست هستند و به علاوه ، دانش و درک او از جبر ، بسیار فراتر از دانش کسانی است که مقاله او را داوری می کنند.
واقعیّت نیز همین بود که داوران آکادمی ، دانش و توانایی فهمیدن استدلال های گالوا را نداشتند. از طرف دیگر ، سنّ کم گالوا که در آن زمان فقط 19 سال داشت و مواجه شدن داوران با دست نوشته ای نا مفهوم و همچنین اعتقادات ضدّ دولتی گالوا ، همه و همه دست به دست هم داده بودند تا مقاله گالوا مورد تأیید آکادمی علوم پاریس قرار نگیرد. به طوری که پواسون در انتهای گزارش خود به آکادمی می نویسد:
« به صورتی که در حال حاضر مقاله به آکادمی ارائه شده ، نمی توانیم تصویب آنرا به شما توصیه کنیم. »
و این یعنی مقاله گالوا رد شده است.
پس از رد شدن مقاله توسط پواسون، گالوا به شدّت ناراحت و تلخ کام شد و بعد از آن برای پروراندن مقاله خود و قابل فهم تر ساختن آن چنانکه پواسون می خواست ، ابداً هیچ کوششی نکرد.
به خاطر این وقایع یا به خاطر آنکه پدرش طرفدار جمهوری بود ، گالوا به انتقاد شدید از رژیم بوربونها دست زد و به گارد ملّی فرانسه یعنی سازمان جمهوری خواهان پیوست. در این زمان ، فرانسه ، سخت گرفتار آشوبهای سیاسی بود. گالوا به خاطر فعالیّت های سیاسی اش محاکمه شد و به عنوان زندانی سیاسی ، چند ماهی را در زندان گذراند.
پس از آزادی از زندان در سال 1832 ، گرفتار عشق دختری عشوه گر شد. امّا گالوای بدشانس در بازی عشق نیز شانس نیاورد و بر سر دستیابی به این دختر ناگزیر به انجام یک دوئل مرگبار شد.
شب قبل از آن دوئل مرگ آفرین ، نامه ای به دوستش "ژوزف لیویل " می نویسد و در آن ، ناگفته ها و یافته های ریاضی اش را به اختصار شرح می دهد و از او می خواهد تا توجّه جهان ریاضی را به اهمیّت کارهایش جلب کند. او حتّی در این نامه از ژاکوبی یا گاوس درخواست می کند که نظرشان را نه در مورد اهمیّت این قضایا ، بلکه در مورد اهمیّت آنها ، بیان کنند.
جمله معروف " من وقت ندارم " را گالوا در یک یادداشت حاشیه ای ، احتمالاً در شب قبل از دوئل ، در ارتباط با برهان گزاره دوّم خود که گفته است نیاز به تکمیل شدن دارد ، نوشته است. چون دیگر وقت کافی برای تکمیل آن برهان نداشت. گرچه در ابتدا ، اثباتش غلط به نظر می رسد.
او درباره دوئلی که فردای آن شب جان او را گرفت نیز می نویسد:
« من قربانی یک زن عشوه گر گمنام شده ام... این یک نزاع اسف بار است که جان مرا می ستاند ... آه! چرا باید برای یک چیز بی ارزش بمیرم ... »
سرانجام ، دوئل در 25 قدمی صورت گرفت. تیر به شکم گالوای بدشانس خورد و به زمین افتاد. ساعت ها در آنجا ماند تا آنکه دهقانی که از آنجا عبور می کرد ، او را به بیمارستان برد.گالوا روز بعد ، یعنی 31 مه 1832 در سنّ 20 سالگی فوت کرد و در بخش عمومی قبرستان مونت پارناس به خاک سپرده شد.
14 سال پس از مرگ گالوا یعنی در سال 1846 ، طرفداران اندکش موفق شدند مخاطبینی برای کارهایش پیدا کنند و به عمق کشفیات او تا حدودی دست یابند. قسمتی از نوشته هایش توسط ژوزف لیویل در مجله ریاضیات به چاپ رسید.
لیویل در اطلاعیه پیش از چاپ کارهای گالوا ، وقتی که فهمیده بود روش هاس گالوا درست بوده اند و می توان قضیه هایش را با دقّت زیاد اثبات کرد ، از آن به عنوان "یک لذّت جاوید در زندگی اش" یاد می کنند. پس از آن ، شناسایی و درک اهمیّت فراوان کارهایش به سرعت آغاز و احترام به گالوا بیشتر شد. شهرت گالوا 14 سال پس از مرگش آغاز شد. به طوری که در حال حاضر یکی از بزرگترین ریاضیدانان خلاّق تمام عصرها به شمار می آید.
او زنده نماند تا به گسترش عمیق تر کاربردها و توسعه ی نظریه خود که بعدها "نظریه گالوا" نام گرفت ، بپردازد. نظریه گالوا امروزه یکی از مباحث مهم و پرکاربرد جبر مجرد و نظریه گروه ها است. حتّی امروز ، ریاضیات در اثر حادثه غم انگیزی که برای او روی داده است ، احتمالاً بضاعت کمتری دارد.







 ) هرگاه یک
) هرگاه یک  وجود داشته باشد.
وجود داشته باشد. 

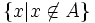
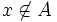 انگاه
انگاه 
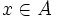 انگاه
انگاه 
 است.
است.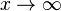 [/img] یعنی متغیر x فراتر از هر مقدار در نظرگرفته شده رشد میکند.
[/img] یعنی متغیر x فراتر از هر مقدار در نظرگرفته شده رشد میکند. نمایش میدهند و میخوانند «الف صفر» (از اولین حرف الفبای عبری بهنام «الف»). این عدد «تعداد» عددهای مجموعه اعداد طبیعی را نشان میدهد، که «بینهایت» است. جالب است که بدانید که عدد اصلی مجموعههای N و Z و Q یکسان هستند ولی عدد اصلی مجموعه R برابر عددی است که آن را الف میخوانند. خوب است بدانید که الف برابر دو به توان الف صفر میباشد. بینهایت دارای دو مفهوم فیزیکی و ریاضی است که کاملاً با یکدیگر متفاوتند.
نمایش میدهند و میخوانند «الف صفر» (از اولین حرف الفبای عبری بهنام «الف»). این عدد «تعداد» عددهای مجموعه اعداد طبیعی را نشان میدهد، که «بینهایت» است. جالب است که بدانید که عدد اصلی مجموعههای N و Z و Q یکسان هستند ولی عدد اصلی مجموعه R برابر عددی است که آن را الف میخوانند. خوب است بدانید که الف برابر دو به توان الف صفر میباشد. بینهایت دارای دو مفهوم فیزیکی و ریاضی است که کاملاً با یکدیگر متفاوتند.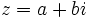 یا
یا 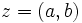 تعریف میشود که در آن
تعریف میشود که در آن 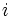 را واحد موهومی مینامند و دارای خاصیت
را واحد موهومی مینامند و دارای خاصیت 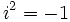
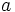 را قسمت حقیقی عدد
را قسمت حقیقی عدد 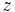 و
و 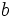 را قسمت موهومی آن گویند و به ترتیب با
را قسمت موهومی آن گویند و به ترتیب با 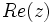 و
و 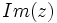 نمایش میدهند.
نمایش میدهند. 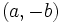 را مزدوج
را مزدوج 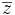 نمایش میدهند . به عبارت دیگر مزدوج
نمایش میدهند . به عبارت دیگر مزدوج  .
.  را مساوی گویند ، اگر و فقط اگر
را مساوی گویند ، اگر و فقط اگر 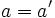 و
و .
.  را
را 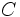 در نظر بگیریم. چرا که اگر
در نظر بگیریم. چرا که اگر 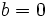 ، آنگاه
، آنگاه  باشد ،
باشد ، 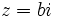 را یک عدد موهومی محض نامند.
را یک عدد موهومی محض نامند. 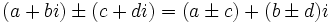
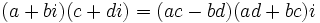
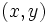 یا
یا  باشد ، آنگاه طبق شکل داریم
باشد ، آنگاه طبق شکل داریم 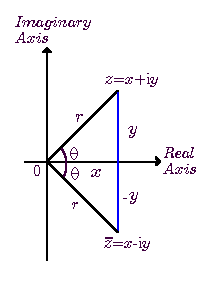
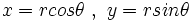
 را
را 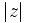 یا
یا 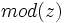 نشان میدهند و
نشان میدهند و  را آرگومان یا فاز عدد
را آرگومان یا فاز عدد  نمایش میدهند که زاویه بین
نمایش میدهند که زاویه بین  با جهت مثبت محور
با جهت مثبت محور  ها است. لذا خواهیم داشت :
ها است. لذا خواهیم داشت : 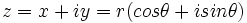
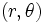 را مختصات قطبی نامند . اغلب ترجیح داده میشود به جای عبارت
را مختصات قطبی نامند . اغلب ترجیح داده میشود به جای عبارت 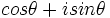 از نماد
از نماد  استفاده شود.
استفاده شود.  داشته باشیم
داشته باشیم  آنگاه روابط زیر برقرارند:
آنگاه روابط زیر برقرارند: 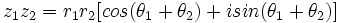


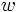 را ریشه
را ریشه  ام عدد مختلط
ام عدد مختلط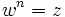 باشد و مینویسند
باشد و مینویسند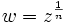 .اگر
.اگر
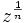 وجود دارد. یعنی
وجود دارد. یعنی 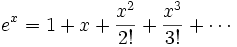
 و نتیجه را مرتب کنیم ، خواهیم داشت:
و نتیجه را مرتب کنیم ، خواهیم داشت: 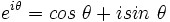
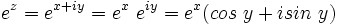
 را میتوان در حوزه اعداد حقیقی حل کرد و چنین نوشت:
را میتوان در حوزه اعداد حقیقی حل کرد و چنین نوشت:  . ولی وضعیت در مورد معادله درجه دوم کاملاً متفاوت است. به عنوان مثال معادله درجه دوم
. ولی وضعیت در مورد معادله درجه دوم کاملاً متفاوت است. به عنوان مثال معادله درجه دوم را در حوزه اعداد حقیقی نمیتوان حل کرد و
را در حوزه اعداد حقیقی نمیتوان حل کرد و
 +7 نا معقول مینماید. و برای کسانی که فقط اعداد صحیح را میشناسد معادلههای
+7 نا معقول مینماید. و برای کسانی که فقط اعداد صحیح را میشناسد معادلههای  و
و  جواب ندارند. اما با توسیع دستگاه اعداد به صورتی که اعدادی منفی، کسری و اصم را نیز در برگیرد، این معادلات به ترتیب جوابهای
جواب ندارند. اما با توسیع دستگاه اعداد به صورتی که اعدادی منفی، کسری و اصم را نیز در برگیرد، این معادلات به ترتیب جوابهای را خواهند داشت.
را خواهند داشت. 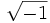 ، یعنی عددی را که مربعش 1- است، نیز در بر گیرد. این گونه اعداد با احساس شهودی ما اصلاً جور در نمیآیند و در گذشته بسیاری از ریاضیدانان با معرفی این گونه هیولاها مخالفت داشتند و از این رو آنها را اعداد انگاری نامیده اند. وضعیت تا سده هیجدهم به همین منوال بود تا اینکه لئونهارت اویلر (1707-1783) با کارهای استادانه روی اعداد انگاری نتایج متعدد جالبی بدست آورد. ک.ف گاوس(1777- 1855 ) با معرفی اعداد انگاری به صورت نقاط یک صفحه نام تازه اعداد مختلط را بر آنها نهاد و از آنها برای یافتن نتایجی چشمگیر از نظریه اعداد استفاده نمود. از این طریق عضویت اعداد مختلط را در سلسه اعداد مسجل ساخت. تقریباً در همان زمان اُ.ل. کوشی ( 1789 – 1857 )، هنگام تلاش در پیدا کردن روشی یکنواخت برای محاسبه انتگرال های معین،حساب دیفرانسیل و انتگرال توابع با متغیرهای مختلط را بررسی کرد. این امر سرآغاز نظریه توابعی بود که زمینه مساعدی برای کشف توابع بیضوی از سوی ن.ه. آبل (1802 – 1829 ) و کارل گوستاو یاکوبی (1804 – 1851) را فراهم ساخت. علاوه بر این، بسط هندسه تصویری نشان داد که استفاده از اعداد مختلط در هندسه نیز امری اجتناب ناپذیر است. پیشرفت تحقیقات روشن کرده است که برای اینکه ریاضیات، حتی فقط حساب دیفرانسیل و انتگرال را به خوبی بفهمیم، محدودیت غیر طبیعی حوزه اعداد حقیقی به ما حکم میکند که برای دستیابی به مفاهیم یکنواختی و همسازی، اعداد مختلط را نیز دخالت دهیم.
، یعنی عددی را که مربعش 1- است، نیز در بر گیرد. این گونه اعداد با احساس شهودی ما اصلاً جور در نمیآیند و در گذشته بسیاری از ریاضیدانان با معرفی این گونه هیولاها مخالفت داشتند و از این رو آنها را اعداد انگاری نامیده اند. وضعیت تا سده هیجدهم به همین منوال بود تا اینکه لئونهارت اویلر (1707-1783) با کارهای استادانه روی اعداد انگاری نتایج متعدد جالبی بدست آورد. ک.ف گاوس(1777- 1855 ) با معرفی اعداد انگاری به صورت نقاط یک صفحه نام تازه اعداد مختلط را بر آنها نهاد و از آنها برای یافتن نتایجی چشمگیر از نظریه اعداد استفاده نمود. از این طریق عضویت اعداد مختلط را در سلسه اعداد مسجل ساخت. تقریباً در همان زمان اُ.ل. کوشی ( 1789 – 1857 )، هنگام تلاش در پیدا کردن روشی یکنواخت برای محاسبه انتگرال های معین،حساب دیفرانسیل و انتگرال توابع با متغیرهای مختلط را بررسی کرد. این امر سرآغاز نظریه توابعی بود که زمینه مساعدی برای کشف توابع بیضوی از سوی ن.ه. آبل (1802 – 1829 ) و کارل گوستاو یاکوبی (1804 – 1851) را فراهم ساخت. علاوه بر این، بسط هندسه تصویری نشان داد که استفاده از اعداد مختلط در هندسه نیز امری اجتناب ناپذیر است. پیشرفت تحقیقات روشن کرده است که برای اینکه ریاضیات، حتی فقط حساب دیفرانسیل و انتگرال را به خوبی بفهمیم، محدودیت غیر طبیعی حوزه اعداد حقیقی به ما حکم میکند که برای دستیابی به مفاهیم یکنواختی و همسازی، اعداد مختلط را نیز دخالت دهیم.  (انگاری) را برای
(انگاری) را برای 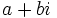 که
که 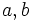 اعدادی هستند حقیقی و محاسبه با آنها همانند محاسبه با اعداد حقیقی است، با در نظر گرفتن اینکه به جای
اعدادی هستند حقیقی و محاسبه با آنها همانند محاسبه با اعداد حقیقی است، با در نظر گرفتن اینکه به جای 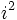 باید،1- قرار داد. مثلاً
باید،1- قرار داد. مثلاً 

 یافتن عددی است مثل
یافتن عددی است مثل 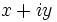 که در تساوی
که در تساوی 

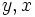 را چنان پیدا کنیم که در روابط
را چنان پیدا کنیم که در روابط  صدق کنند. این دستگاه معادلات یک جواب یکتای زیر را دارد.
صدق کنند. این دستگاه معادلات یک جواب یکتای زیر را دارد. 
 . بنابراین
. بنابراین 
 نیز به دست آوریم.
نیز به دست آوریم.  ویافتن
ویافتن  همانند حاصل جمع
همانند حاصل جمع  با 4 کیلوگرم و یافتن
با 4 کیلوگرم و یافتن  نیست؟ همین طور،
نیست؟ همین طور،  نیز دو جواب دارد که جواب دارد که جواب مثبت آن 1 است و جواب دیگر آن 1- . اما آیا گفتن نامثبت است معنی دارد؟
نیز دو جواب دارد که جواب دارد که جواب مثبت آن 1 است و جواب دیگر آن 1- . اما آیا گفتن نامثبت است معنی دارد؟  نمایانده میشود، با ویژگیهای زیرین:
نمایانده میشود، با ویژگیهای زیرین: 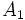 : قانون جابجایی : به ازای هر دو عدد
: قانون جابجایی : به ازای هر دو عدد  ،
، 
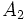 : قانون شرکتپذیری: به ازای هرسه عدد
: قانون شرکتپذیری: به ازای هرسه عدد
 : عنصر همانی در جمع : عدد حقیقی یکتایی که با
: عنصر همانی در جمع : عدد حقیقی یکتایی که با نمایانده میشود وجود دارد چنان که:
نمایانده میشود وجود دارد چنان که: 

 : عکس جمعی : به ازای هر عدد
: عکس جمعی : به ازای هر عدد 
 نمایش میدهند.
نمایش میدهند. 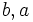 منحصراً یک عدد سومی به نام حاصلضرب را مشخص میسازند که با
منحصراً یک عدد سومی به نام حاصلضرب را مشخص میسازند که با  نمایش داده میشود، با ویژگیهای زیرین:
نمایش داده میشود، با ویژگیهای زیرین:  : قانون جابه جایی: به ازای همه مقادیر
: قانون جابه جایی: به ازای همه مقادیر 
 : قانون شرکت پذیری: به ازای همه مقادیر
: قانون شرکت پذیری: به ازای همه مقادیر ،
، 
 : عنصر همانی در ضرب: عدد حقیقی یکتایی وجود دارد که با 1 نمایانده میشود، به طوری که به ازای همه مقادیر
: عنصر همانی در ضرب: عدد حقیقی یکتایی وجود دارد که با 1 نمایانده میشود، به طوری که به ازای همه مقادیر 
 : عکس ضربی: به ازای هر
: عکس ضربی: به ازای هر عدد یکتایی مانند
عدد یکتایی مانند
 یا
یا نشان میدهند.
نشان میدهند. 
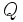 مرکب از تمام اعداد گویا یک هیات است، ولی نه مجموعه همه اعداد درست
مرکب از تمام اعداد گویا یک هیات است، ولی نه مجموعه همه اعداد درست 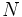 .
. 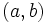 از اعداد حقیقی است با ویژگیهای زیر: دو عدد مختلط
از اعداد حقیقی است با ویژگیهای زیر: دو عدد مختلط  فقط و فقط وقتی برابرند که
فقط و فقط وقتی برابرند که  . مجموع و حاصلضرب دو عدد مختلط
. مجموع و حاصلضرب دو عدد مختلط 




 را در نظر میگیریم، پس
را در نظر میگیریم، پس 


 )
) 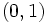 را در نظر میگیریم. داریم
را در نظر میگیریم. داریم 
 نیز 1- است، ولی چنانچه بنویسیم
نیز 1- است، ولی چنانچه بنویسیم  ، آن گاه عدد مختلط دلخواه
، آن گاه عدد مختلط دلخواه 
 ،
،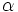 مینامند و آن را با
مینامند و آن را با  نمایش میدهند؛ همین طور
نمایش میدهند؛ همین طور نشان میدهند. از این رو اعداد حقیقی، اعداد مختلطی هستند که جزء انگاری آنها
نشان میدهند. از این رو اعداد حقیقی، اعداد مختلطی هستند که جزء انگاری آنها عدد مختلط
عدد مختلط  را مزدوج مختلط
را مزدوج مختلط نمایش می دهند. به آسانی میتوان روابط زیررا تحقیق نمود:
نمایش می دهند. به آسانی میتوان روابط زیررا تحقیق نمود: 




 ، حاصلضرب
، حاصلضرب  همواره عددی حقیق و نامنفی است. ریشه دوم نامنفی این عدد را کالبد یا قدر مطلق عدد مختلط
همواره عددی حقیق و نامنفی است. ریشه دوم نامنفی این عدد را کالبد یا قدر مطلق عدد مختلط  نمایش میدهند. از این رو
نمایش میدهند. از این رو 
 ، اگر و فقط اگر
، اگر و فقط اگر  .
.  ، پس
، پس  بنابراین
بنابراین 
 بنابراین
بنابراین 
 مستلزم تساوی های
مستلزم تساوی های  نیست. مثلاً اگر بنویسیم
نیست. مثلاً اگر بنویسیم  ، آنگاه
، آنگاه 
 )
)
 )
) 




 اعداد حقیقی اند
اعداد حقیقی اند 
 ولی
ولی و
و  به صورت
به صورت 






 ، در
، در 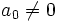 ) گویند. از قضیه بنیادی جبر نتیجه میشود که:
) گویند. از قضیه بنیادی جبر نتیجه میشود که:  را حل کنید.
را حل کنید.  ، پس، چون
، پس، چون 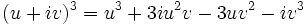
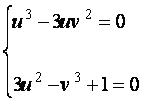
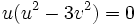
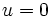 یا
یا 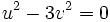
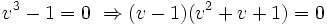
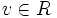 ،
، 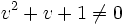 ، لذا
، لذا 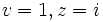 . هنگامی که
. هنگامی که  ،
، 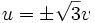 . از قرار دادن این مقدار در معادله دوم خواهیم داشت
. از قرار دادن این مقدار در معادله دوم خواهیم داشت 

 و لذا
و لذا 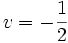 پس
پس 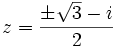 و
و 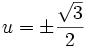

 در حال حرکت است بنابراین شتاب مماس آن یعنی
در حال حرکت است بنابراین شتاب مماس آن یعنی  صفر است و در نتیجه شتاب کلی آن تنها شتاب مرکز گرای آن
صفر است و در نتیجه شتاب کلی آن تنها شتاب مرکز گرای آن  است(
است( شعاع خمیدگی مسیر است که برای شکل بالا بر روی مسیر خمیده مقداری برابر R دارد).بنابراین اندازه شتاب بر روی مسیر مستقیم صفر است و در مسیر نیم دایره
شعاع خمیدگی مسیر است که برای شکل بالا بر روی مسیر خمیده مقداری برابر R دارد).بنابراین اندازه شتاب بر روی مسیر مستقیم صفر است و در مسیر نیم دایره  است.به این دلیل مقدار شتاب در نقاط A,B,C,D نا پیوسته است (همانطور که در نمودار مشخص است). همین نا پیوستگی سبب می شود تا نیروی عکس العملی که از جانب قطار به ریل وارد می شود نیز در این نقاط نا پیوسته باشد . به همین دلیل نوعی شوک یا ضربه به هنگام وارد شدن و یا ترک پیچ وجود دارد ( البته حتما اثر این ضربه را در پیچ های غیر اصولی هنگام عبور خودرو و یا برعکس نیروی نرم و یکنواختی را در هنگام سفر در داخل مترو حس کرده اید) برای جلوگیری از بوجود آمدن چنین نقاط فشاری که موجب خروج قطار از ریل و یا خروج خودرو از جاده می شود مسیرها می بایست طوری طراحی شوند که خمیدگی جاده بطور یکنواخت تغییر کند.( البته این طراحی بطور نسبی و با توجه به شرایط محیطی و کمک گرفتن از شیب و اتصالات قوی تر نیز قابل بهبود است )
است.به این دلیل مقدار شتاب در نقاط A,B,C,D نا پیوسته است (همانطور که در نمودار مشخص است). همین نا پیوستگی سبب می شود تا نیروی عکس العملی که از جانب قطار به ریل وارد می شود نیز در این نقاط نا پیوسته باشد . به همین دلیل نوعی شوک یا ضربه به هنگام وارد شدن و یا ترک پیچ وجود دارد ( البته حتما اثر این ضربه را در پیچ های غیر اصولی هنگام عبور خودرو و یا برعکس نیروی نرم و یکنواختی را در هنگام سفر در داخل مترو حس کرده اید) برای جلوگیری از بوجود آمدن چنین نقاط فشاری که موجب خروج قطار از ریل و یا خروج خودرو از جاده می شود مسیرها می بایست طوری طراحی شوند که خمیدگی جاده بطور یکنواخت تغییر کند.( البته این طراحی بطور نسبی و با توجه به شرایط محیطی و کمک گرفتن از شیب و اتصالات قوی تر نیز قابل بهبود است )
 نتیجه شود و بنابراین
نتیجه شود و بنابراین  و شتاب کل
و شتاب کل 



 با توجه به شكل 65 با 64 برابر است.
با توجه به شكل 65 با 64 برابر است. منطقي كه تكنيك را هوشمند كرد
منطقي كه تكنيك را هوشمند كرد 












 من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.
من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.