یک عدد مختلط به صورت 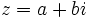 یا
یا 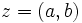 تعریف میشود که در آن
تعریف میشود که در آن ![]()
دو عدد حقیقی اند.در این نمایش 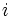 را واحد موهومی مینامند و دارای خاصیت
را واحد موهومی مینامند و دارای خاصیت 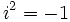
میباشد. 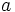 را قسمت حقیقی عدد
را قسمت حقیقی عدد 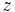 و
و 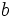 را قسمت موهومی آن گویند و به ترتیب با
را قسمت موهومی آن گویند و به ترتیب با 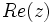 و
و 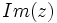 نمایش میدهند.
نمایش میدهند.
مزدوج عدد مختلط
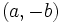 را مزدوج
را مزدوج 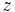 نامیده و با
نامیده و با 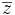 نمایش میدهند . به عبارت دیگر مزدوج
نمایش میدهند . به عبارت دیگر مزدوج 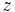 عبارت است از
عبارت است از  .
. تساوی دو عدد مختلط
دو عدد مختلط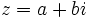 و
و  را مساوی گویند ، اگر و فقط اگر
را مساوی گویند ، اگر و فقط اگر 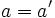 و
و .
. نکته
می توانیم مجموعه اعداد حقیقی را زیرمجموعه اعداد مختلط
را زیرمجموعه اعداد مختلط 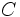 در نظر بگیریم. چرا که اگر
در نظر بگیریم. چرا که اگر 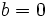 ، آنگاه
، آنگاه 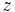 یک عدد حقیقی خواهد بود. حال اگر
یک عدد حقیقی خواهد بود. حال اگر  باشد ،
باشد ، 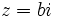 را یک عدد موهومی محض نامند.
را یک عدد موهومی محض نامند. عملیات اساسی با اعداد مختلط
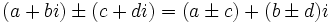
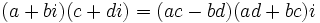
شکل مثلثاتی یا قطبی اعداد مختلط
اگر 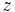 نقطه ای از صفحه مختلط ، متناظر به عدد
نقطه ای از صفحه مختلط ، متناظر به عدد 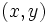 یا
یا  باشد ، آنگاه طبق شکل داریم
باشد ، آنگاه طبق شکل داریم
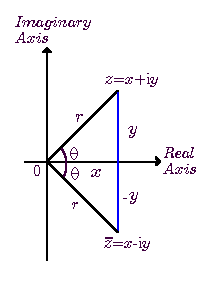
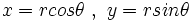
که در آن  را قدر مطلق یا نرم یا مدول عدد مختلط
را قدر مطلق یا نرم یا مدول عدد مختلط  گویند و با
گویند و با 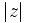 یا
یا 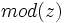 نشان میدهند و
نشان میدهند و  را آرگومان یا فاز عدد
را آرگومان یا فاز عدد 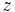 گویند و با
گویند و با  نمایش میدهند که زاویه بین
نمایش میدهند که زاویه بین  با جهت مثبت محور
با جهت مثبت محور  ها است. لذا خواهیم داشت :
ها است. لذا خواهیم داشت :
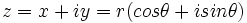
وآن را شکل مثلثاتی یا قطبی عدد مختلط گویند و 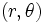 را مختصات قطبی نامند . اغلب ترجیح داده میشود به جای عبارت
را مختصات قطبی نامند . اغلب ترجیح داده میشود به جای عبارت 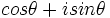 از نماد
از نماد  استفاده شود.
استفاده شود.
قضیه دموآر
اگر به ازای  داشته باشیم
داشته باشیم  آنگاه روابط زیر برقرارند:
آنگاه روابط زیر برقرارند:
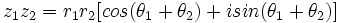

و از تعمیم آن خواهیم داشت:

ریشه های اعداد مختلط
عدد مختلط 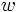 را ریشه
را ریشه  ام عدد مختلط
ام عدد مختلط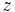 گویند ، اگر
گویند ، اگر 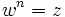 باشد و مینویسند
باشد و مینویسند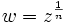 .اگر
.اگر عددی صحیح و مثبت باشد ، میتوان به کمک قضیه دموآر نشان داد که:
عددی صحیح و مثبت باشد ، میتوان به کمک قضیه دموآر نشان داد که:

از اینجا نتیجه میشود که  مقدار مختلف برای
مقدار مختلف برای 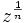 وجود دارد. یعنی
وجود دارد. یعنی 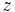 به شرط ناصفر بودن ،
به شرط ناصفر بودن ، ریشه
ریشه  ام مختلف دارد.
ام مختلف دارد.
فرمول اویلر
می دانیم که:
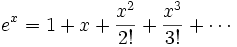
اگر قرار دهیم  و نتیجه را مرتب کنیم ، خواهیم داشت:
و نتیجه را مرتب کنیم ، خواهیم داشت:
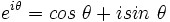
که این فرمول را فرمول اویلر گویند . در حالت کلی :
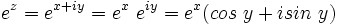
 من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.
من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.