سری های فوریه
|
 |
توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است.
سری فوریه برای بررسی حرکات تناوبی در آگوستیک یا صوت شناسی،الکترو دینامیک ،ایتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است.
در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد.
پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود.
تعریف
سری توابع 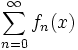 که جمله عمومی آن
که جمله عمومی آن 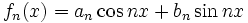 با ضرایب ثابت
با ضرایب ثابت  و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی  ی را نشان میدهد.
ی را نشان میدهد.
این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد.
از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن، ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب
،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب  و
و  و تابع مجموع
و تابع مجموع  به دست آورد.ضرب سری
به دست آورد.ضرب سری  در عاملهای کراندار
در عاملهای کراندار 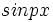 یا
یا 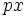 که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
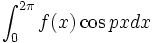 و
و 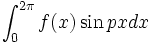 را با استفاده از انتگرالگیری جمله به جمله سری
را با استفاده از انتگرالگیری جمله به جمله سری 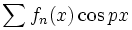 یا
یا 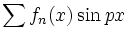 محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه
محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه 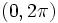 توابع
توابع 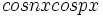 و
و 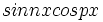 و
و 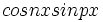 و
و 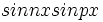 اند.
اند.
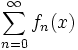 که جمله عمومی آن
که جمله عمومی آن 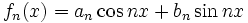 با ضرایب ثابت
با ضرایب ثابت  و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی  ی را نشان میدهد.
ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد.
از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن،
 ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب
،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب  و
و  و تابع مجموع
و تابع مجموع  به دست آورد.ضرب سری
به دست آورد.ضرب سری  در عاملهای کراندار
در عاملهای کراندار 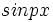 یا
یا 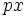 که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان 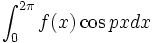 و
و 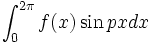 را با استفاده از انتگرالگیری جمله به جمله سری
را با استفاده از انتگرالگیری جمله به جمله سری 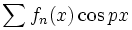 یا
یا 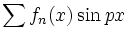 محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه
محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه 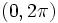 توابع
توابع 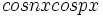 و
و 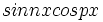 و
و 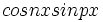 و
و 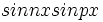 اند.
اند. 
سری فوریه ، روشی در ریاضیات میباشد که به وسیله آن ، هر تابع متناوبی به صورت جمعی از توابع سینوس و کسینوس میتواند نوشته شود. نام این قضیه به اسم ریاضیدان فرانسوی ، ژوزف فوریه ،ثبت شده است.
در نظریه سریهای فوریه نشان داده شده است که اگر (f(x در شرایطی مثل (شرط دیریشله) صدق کند، میتوان آن را به صورت سری هماهنگی به شکل:
بسط داد و اینکه در نقاط ناپیوستگی سری سمت راست رابطه فوق برابر مقدار متوسط است. ضرایب an و bn را میتوان با استفاده از روابط متعامد:
که در آنها mnδ نماد کرونکر است که به ازای m=n برابر واحد و در غیر اینصورت صفر است. همچنین اگر یک تابع متناوب با تناوب T باشد یا به عبارتی: (f(t + T) = f(t آنگاه ، این تابع به صورت زیر میتواند نوشته شود:
در اینجا داریم:
سری فوریه میتواند به صورت زیر نیز نوشته شود:
که
حساب کرد. میتوان نشان داد که این سری به طور یکنواخت در بازه (L/۲ , -L/۲) همگراست، بطوری که انتگرال گیری جمله به جمله در استنتاج این معادلات کار بجایی است. این معادلات را با تبدیلات زیر ادامه میدهیم:
در نتیجه:
بنابراین:
حال با تغییر بازه انتگرال گیر فوق به {o,2L} داریم:
این سری را میتوان به صورت زیر هم نوشت:
به عنوان آزمون:
بنابراین:
ضریب An را میتوان به صورت زیر توسعه داد:
در نهایت در بازه {L/2 , L/2-} سری فوریه به صورت:
و
تعریف میشود.
+ نوشته شده در شنبه بیست و دوم دی ۱۳۸۶ ساعت 15:20 توسط كاوه آهنگر بيك
|
 من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.
من کاوه هستم,اهل تهران.در دانشگاه باهنر کرمان درس می خونم.اصلیتم خراسان شمالی است.رشته ام علوم کامپیوتره.ولی به خاطر علاقه ام به ریاضی تصمیم گرفتم تا وبلاگی در مورد مسائل ریاضی ایجاد کنم.امیدوارم از وبلاگ من راضی باشید.